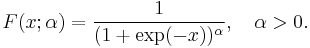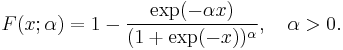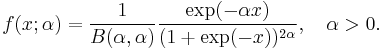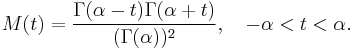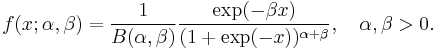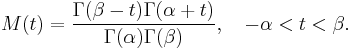Generalized logistic distribution

The term generalized logistic distribution is used as the name for several different families of probability distributions. For example, Johnson et al.[1] list four forms, which are listed below. One family described here has also been called the skew-logistic distribution. For other families of distributions that have also been called generalized logistic distributions, see the shifted log-logistic distribution, which is a generalization of the log-logistic distribution.

Contents

Definitions

The following definitions are for standardized versions of the families, which can be expanded to the full form as a location-scale family. Each is defined using either the cumulative distribution function (F) or the probability density function (ƒ), and is defined on (-∞,∞).

Type I

F(x;\alpha)=\frac{1}{(1%2B\exp(-x))^\alpha}, \quad \alpha > 0 .

This type has also been called the "skew-logistic" distribution.

Type II

F(x;\alpha)=1-\frac{\exp(-\alpha x)}{(1%2B\exp(-x))^\alpha}, \quad \alpha > 0 .

Type III

f(x;\alpha)=\frac{1}{B(\alpha,\alpha)}\frac{\exp(-\alpha x)}{(1%2B\exp(-x))^{2\alpha}}, \quad \alpha > 0 .

Here B is the beta function. The moment generating function for this type is

M(t)=\frac{\Gamma(\alpha-t) \Gamma(\alpha%2Bt) }{ (\Gamma(\alpha))^2 }, \quad -\alpha<t<\alpha.

Type IV

f(x;\alpha,\beta)=\frac{1}{B(\alpha,\beta)}\frac{\exp(-\beta x)}{(1%2B\exp(-x))^{\alpha%2B\beta}}, \quad \alpha,\beta > 0 .

Again, B is the beta function. The moment generating function for this type is

M(t)=\frac{\Gamma(\beta-t) \Gamma(\alpha%2Bt) }{ \Gamma(\alpha) \Gamma(\beta) }, \quad -\alpha<t<\beta.

This type is also called the "exponential generalized beta of the second type".[1]

References

  1. ^ a b Johnson, N.L., Kotz, S., Balakrishnan, N. (1995) Continuous Univariate Distributions, Volume 2, Wiley. ISBN 0-471-58494-0 (pages 140–142)